Matura 2016 czerwiec
Liczba \(\frac{7^6\cdot 6^7}{42^6}\) jest równa
A.\( 42^{36} \)
B.\( 42^7 \)
C.\( 6 \)
D.\( 1 \)
Cenę pewnego towaru podwyższono o \(20\%\), a następnie nową cenę tego towaru podwyższono o \(30\%\). Takie dwie podwyżki ceny tego towaru można zastąpić równoważną im jedną podwyżką
A.o \( 50\% \)
B.o \( 56\% \)
C.o \( 60\% \)
D.o \( 66\% \)
Liczba \(\sqrt[3]{3\sqrt{3}}\) jest równa
A.\( \sqrt[6]{3} \)
B.\( \sqrt[4]{3} \)
C.\( \sqrt[3]{3} \)
D.\( \sqrt{3} \)
Różnica \(50001^2 - 49999^2\) jest równa
A.\( 2\ 000\ 000 \)
B.\( 200\ 000 \)
C.\( 20\ 000 \)
D.\( 4 \)
Najmniejsza wartość wyrażenia \((x-y)(x+y)\) dla \(x,y\in \{2,3,4\}\) jest równa
A.\( 2 \)
B.\( -24 \)
C.\( 0 \)
D.\( -12 \)
Wartość wyrażenia \(\log_3\frac{3}{2}+\log_3\frac{2}{9}\) jest równa
A.\( -1 \)
B.\( -2 \)
C.\( \log_3\frac{5}{11} \)
D.\( \log_3\frac{31}{18} \)
Spośród liczb, które są rozwiązaniami równania \((x-8)(x^2-4)(x^2+16)=0\) wybrano największą i najmniejszą. Suma tych dwóch liczb jest równa
A.\( 12 \)
B.\( 10 \)
C.\( 6 \)
D.\( 4 \)
Rozwiązaniem równania \(\frac{x-7}{x}=5\), gdzie \(x\ne 0\) jest liczba należąca do przedziału
A.\( (-\infty ,-2) \)
B.\( \langle -2,-1) \)
C.\( \langle -1,0) \)
D.\( (0,+\infty ) \)
Funkcja \(f\) określona jest wzorem \(f(x)=\frac{2x^3}{x^4+1}\) dla każdej liczby rzeczywistej \(x\). Wtedy liczba \(f(-\sqrt{2})\) jest równa
A.\( -\frac{8}{5} \)
B.\( -\frac{4\sqrt{2}}{3} \)
C.\( -\frac{4\sqrt{2}}{5} \)
D.\( -\frac{4}{3} \)
Dana jest funkcja kwadratowa \(f(x)=-2(x+5)(x-11)\). Wskaż maksymalny przedział, w którym funkcja \(f\) jest rosnąca.
A.\( (-\infty ,3\rangle \)
B.\( (-\infty ,5\rangle \)
C.\( (-\infty ,11\rangle \)
D.\( \langle 6,+\infty ) \)
Ciąg \((a_n)\) jest określony wzorem \(a_n=6(n-16)\) dla \(n\ge 1\). Suma dziesięciu początkowych wyrazów tego ciągu jest równa
A.\( -54 \)
B.\( -126 \)
C.\( -630 \)
D.\( -270 \)
Dany jest ciąg geometryczny \((a_n)\), w którym \(a_1=72\) i \(a_4=9\). Iloraz \(q\) tego ciągu jest równy
A.\( q=\frac{1}{2} \)
B.\( q=\frac{1}{6} \)
C.\( q=\frac{1}{4} \)
D.\( q=\frac{1}{8} \)
Dany jest trapez \(ABCD\), w którym przekątna \(AC\) jest prostopadła do ramienia \(BC\), \(|AD|=|DC|\) oraz \(|\sphericalangle ABC|=50^\circ \) (zobacz rysunek). 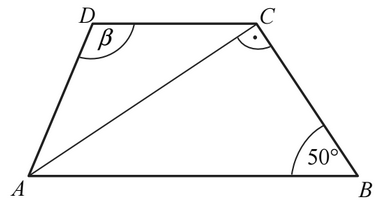 Stąd wynika, że
Stąd wynika, że
 Stąd wynika, że
Stąd wynika, że A.\( \beta =100^\circ \)
B.\( \beta =120^\circ \)
C.\( \beta =110^\circ \)
D.\( \beta =130^\circ \)
Punkty \(A\), \(B\), \(C\) i \(D\) leżą na okręgu o środku \(O\) (zobacz rysunek). Miary zaznaczonych kątów \(\alpha \) i \(\beta \) są odpowiednio równe 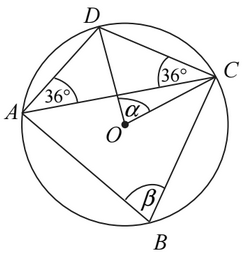

A.\( \alpha =36^\circ,\ \beta =72^\circ \)
B.\( \alpha =54^\circ,\ \beta =72^\circ \)
C.\( \alpha =36^\circ,\ \beta =108^\circ \)
D.\( \alpha =72^\circ,\ \beta =72^\circ \)
Słoń waży \(5\) ton, a waga mrówki jest równa \(0{,}5\) grama. Ile razy słoń jest cięższy od mrówki?
A.\( 10^6 \)
B.\( 10^7 \)
C.\( 10 \)
D.\( 10^8 \)
Każde z ramion trójkąta równoramiennego ma długość \(20\). Kąt zawarty między ramionami tego trójkąta ma miarę \(150^\circ \). Pole tego trójkąta jest równe
A.\( 100 \)
B.\( 200 \)
C.\( 100\sqrt{3} \)
D.\( 100\sqrt{2} \)
Prosta określona wzorem \(y=ax+1\) jest symetralną odcinka \(AB\), gdzie \(A=(-3,2)\) i \(B=(1,4)\). Wynika stąd, że
A.\( a=-\frac{1}{2} \)
B.\( a=\frac{1}{2} \)
C.\( a=-2 \)
D.\( a=2 \)
Układ równań \(\begin{cases} y=-ax+2a \\ y=\frac{b}{3}x-2 \end{cases} \) nie ma rozwiązań dla
A.\( a=-1 \) i \(b=-3\)
B.\( a=1 \) i \(b=3 \)
C.\( a=1 \) i \(b=-3 \)
D.\( a=-1 \) i \(b=3 \)
Do pewnej liczby \(a\) dodano \(54\). Otrzymaną sumę podzielono przez \(2\). W wyniku tego działania otrzymano liczbę dwa razy większą od liczby \(a\). Zatem
A.\( a=27 \)
B.\( a=18 \)
C.\( a=24 \)
D.\( a=36 \)
Podstawą ostrosłupa prawidłowego czworokątnego \(ABCDS\) jest kwadrat \(ABCD\). Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi. Miara kąta \(ASC\) jest równa
A.\( 45^\circ \)
B.\( 30^\circ \)
C.\( 75^\circ \)
D.\( 90^\circ \)
Rzucamy trzy razy symetryczną monetą. Niech \(p\) oznacza prawdopodobieństwo otrzymania dokładnie jednego orła w tych trzech rzutach. Wtedy
A.\( 0\le p\le 0{,}25 \)
B.\( 0{,}25\le p\le 0{,}4 \)
C.\( 0{,}4\le p\le 0{,}5 \)
D.\( p\gt 0{,}5 \)
Średnia arytmetyczna czterech liczb: \(x−1,\ 3x,\ 5x+1\) i \(7x\) jest równa \(72\). Wynika stąd, że
A.\( x=9 \)
B.\( x=10 \)
C.\( x=17 \)
D.\( x=18 \)
Na rysunku przedstawione są dwie proste równoległe \(k\) i \(l\) o równaniach \(y=ax+b\) oraz \(y=mx+n\). Początek układu współrzędnych leży między tymi prostymi. 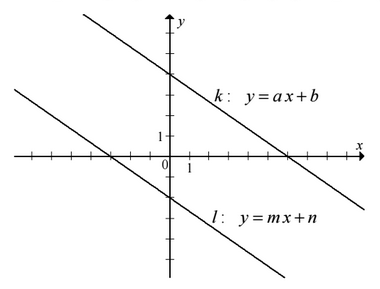 Zatem
Zatem
 Zatem
Zatem A.\( a\cdot m\gt 0 \) i \(b\cdot n\gt 0\)
B.\( a\cdot m\gt 0 \) i \(b\cdot n\lt 0\)
C.\( a\cdot m\lt 0 \) i \(b\cdot n\gt 0\)
D.\( a\cdot m\lt 0 \) i \(b\cdot n\lt 0\)
Dane są dwie sumy algebraiczne \(3x^3-2x\) oraz \(-3x^2-2\). Iloczyn tych sum jest równy
A.\( -9x^5+4x \)
B.\( -9x^6+6x^3-6x^2+4x \)
C.\( -9x^5+6x^3-6x^2+4x \)
D.\( -9x^6+4x \)
Punkty \(D\) i \(E\) są środkami przyprostokątnych \(AC\) i \(BC\) trójkąta prostokątnego \(ABC\). Punkty \(F\) i \(G\) leżą na przeciwprostokątnej \(AB\) tak, że odcinki \(DF\) i \(EG\) są do niej prostopadłe (zobacz rysunek). Pole trójkąta \(BGE\) jest równe \(1\), a pole trójkąta \(AFD\) jest równe \(4\). 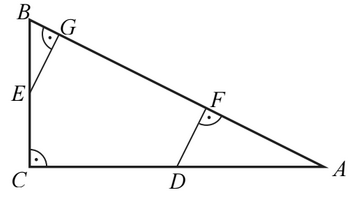 Zatem pole trójkąta \(ABC\) jest równe
Zatem pole trójkąta \(ABC\) jest równe
 Zatem pole trójkąta \(ABC\) jest równe
Zatem pole trójkąta \(ABC\) jest równe A.\( 12 \)
B.\( 16 \)
C.\( 18 \)
D.\( 20 \)
Rozwiąż równanie \(\frac{2x+1}{2x}=\frac{2x+1}{x+1}\), gdzie \(x\ne -1\) i \(x\ne 0\).
Dane są proste o równaniach \(y=x+2\) oraz \(y=-3x+b\), które przecinają się w punkcie leżącym na osi \(Oy\) układu współrzędnych. Oblicz pole trójkąta, którego dwa boki zawierają się w danych prostych, a trzeci jest zawarty w osi \(Ox\).
Wykaż, że dla dowolnych liczb rzeczywistych \(x\), \(y\) prawdziwa jest nierówność \[x^4+y^4+x^2+y^2\ge 2(x^3+y^3)\]
Dany jest trapez prostokątny \(ABCD\) o podstawach \(AB\) i \(CD\) oraz wysokości \(AD\). Dwusieczna kąta \(ABC\) przecina ramię \(AD\) w punkcie \(E\) oraz dwusieczną kąta \(BCD\) w punkcie \(F\) (zobacz rysunek). 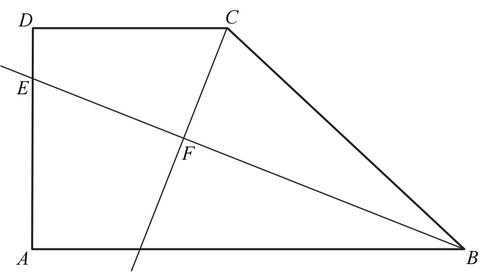 Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.
Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.
 Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.
Wykaż, że w czworokącie \(CDEF\) sumy miar przeciwległych kątów są sobie równe.W trójkącie \(ABC\) dane są długości boków \(|AB|=15\) i \(|AC|=12\) oraz \(\cos \alpha =\frac{4}{5}\), gdzie \(\alpha =\sphericalangle BAC\). Na bokach \(AB\) i \(AC\) tego trójkąta obrano punkty odpowiednio \(D\) i \(E\) takie, że \(|BD|=2|AD|\) i \(|AE|=2|CE|\)(zobacz rysunek). 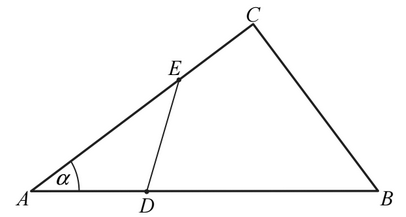 Oblicz pole
Oblicz pole
 Oblicz pole
Oblicz pole trójkąta \(ADE\).
czworokąta \(BCED\).
Dany jest ciąg arytmetyczny \((a_n)\) określony dla każdej liczby naturalnej \(n\ge 1\), w którym \(a_1+a_2+a_3+a_4=2016\) oraz \(a_5+a_6+a_7+...+a_{12}=2016\). Oblicz pierwszy wyraz, różnicę oraz najmniejszy dodatni wyraz ciągu \((a_n)\).
Dany jest stożek o objętości \(8\pi \), w którym stosunek wysokości do promienia podstawy jest równy \(3:8\). Oblicz pole powierzchni bocznej tego stożka.
Rejsowy samolot z Warszawy do Rzymu przelatuje nad Austrią każdorazowo tą samą trasą z taką samą zakładaną prędkością przelotową. We wtorek jego średnia prędkość była o \(10\%\) większa niż prędkość przelotowa, a w czwartek średnia prędkość była o \(10\%\) mniejsza od zakładanej prędkości przelotowej. Czas przelotu nad Austrią w czwartek różnił się od wtorkowego o \(12\) minut. Jak długo trwał przelot tego samolotu nad Austrią we wtorek?