Matura 2013 maj

Wskaż rysunek, na którym zaznaczony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność \(|x + 4| \lt 5\)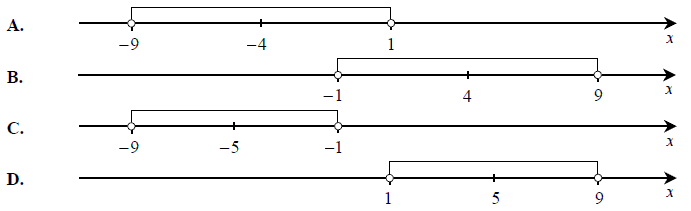

Liczby \(a\) i \(b\) są dodatnie oraz \(12\%\) liczby \(a\) jest równe \(15\%\) liczby \(b\). Stąd wynika, że \(a\) jest równe

Liczba \(\log 100-\log_{2}8\) jest równa

Rozwiązaniem układu równań \(\begin{cases} 5x+3y=3\\ 8x-6y=48 \end{cases} \)   jest para liczb

Punkt \(A=(0, 1)\) leży na wykresie funkcji liniowej \(f(x)=(m-2)x+m-3\). Stąd wynika, że

Wierzchołkiem paraboli o równaniu \(y=-3(x-2)^2+4\) jest punkt o współrzędnych

Dla każdej liczby rzeczywistej \(x\), wyrażenie \(4x^2-12x+9\) jest równe

Prosta o równaniu \(y=\frac{2}{m}x+1\) jest prostopadła do prostej o równaniu \(y=-\frac{3}{2}x-1\). Stąd wynika, że

Na rysunku przedstawiony jest fragment wykresu pewnej funkcji liniowej \(y=ax+b\). 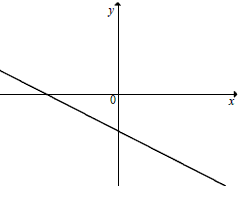Jakie znaki mają współczynniki \(a\) i \(b\)?

Najmniejszą liczbą całkowitą spełniającą nierówność \(\frac{x}{2}\le \frac{2x}{3}+\frac{1}{4}\) jest

Na rysunku 1 przedstawiony jest wykres funkcji \(y=f(x)\) określonej dla \(x\in [-7, 4]\). 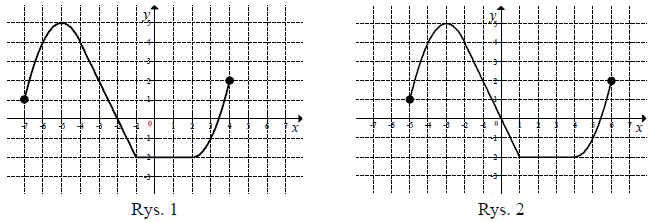Rysunek 2 przedstawia wykres funkcji

Ciąg \((27, 18, x+5)\) jest geometryczny. Wtedy

Ciąg \((a_n)\) określony dla \(n\ge 1\) jest arytmetyczny oraz \(a_3=10\) i \(a_4=14\). Pierwszy wyraz tego ciągu jest równy

Kąt \(\alpha \) jest ostry i \(\sin \alpha =\frac{\sqrt{3}}{2}\). Wartość wyrażenia \(\cos^2\alpha -2\) jest równa

Średnice \(AB\) i \(CD\) okręgu o środku \(S\) przecinają się pod kątem \(50^\circ\) (tak jak na rysunku). 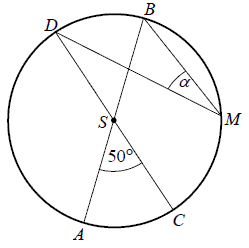Miara kąta \(\alpha \) jest równa

Liczba rzeczywistych rozwiązań równania \((x+1)(x+2)(x^2+3)=0\) jest równa

Punkty \(A=(-1, 2)\) i \(B=(5, -2)\) są dwoma sąsiednimi wierzchołkami rombu \(ABCD\). Obwód tego rombu jest równy

Punkt \(S=(-4, 7)\) jest środkiem odcinka \(PQ\), gdzie \(Q=(17, 12)\). Zatem punkt \(P\) ma współrzędne

Odległość między środkami okręgów o równaniach \((x+1)^2+(y-2)^2=9\) oraz \(x^2+y^2=10\) jest równa

Liczba wszystkich krawędzi graniastosłupa jest o \(10\) większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest

Pole powierzchni bocznej stożka o wysokości \(4\) i promieniu podstawy \(3\) jest równe

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Niech \(p\) oznacza prawdopodobieństwo zdarzenia, że iloczyn liczb wyrzuconych oczek jest równy \(5\). Wtedy

Liczba \(\frac{\sqrt{50}-\sqrt{18}}{\sqrt{2}}\) jest równa

Mediana uporządkowanego niemalejąco zestawu sześciu liczb: \(1, 2, 3, x, 5, 8\) jest równa \(4\). Wtedy

Objętość graniastosłupa prawidłowego trójkątnego o wysokości \(7\) jest równa \(28\sqrt{3}\) . Długość krawędzi podstawy tego graniastosłupa jest równa

Rozwiąż równanie \(x^3+2x^2-8x-16=0\).

Kąt \(\alpha \) jest ostry i \(\sin \alpha =\frac{\sqrt{3}}{2}\). Oblicz wartość wyrażenia \(\sin^2\alpha - 3\cos^2\alpha \).

Udowodnij, że dla dowolnych liczb rzeczywistych \(x, y, z\) takich, że \(x+y+z=0\), prawdziwa jest nierówność \(xy+yz+zx\le 0\).
Możesz skorzystać z tożsamości \((x+y+z)^2=x^2+y^2+z^2+2xy+2xz+2yz .\)

Na rysunku przedstawiony jest wykres funkcji \(f(x)\) określonej dla \(x\in [-7, 8]\). 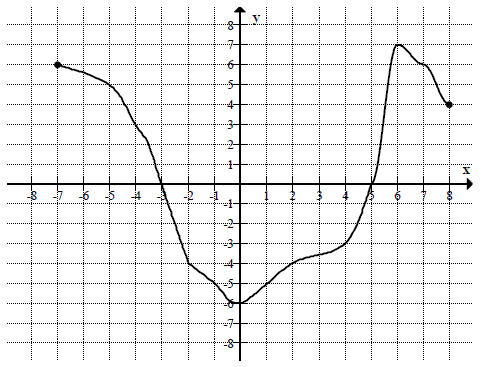Odczytaj z wykresu i zapisz:
  a) największą wartość funkcji \(f\),
  b) zbiór rozwiązań nierówności \(f(x)\lt 0\).

Rozwiąż nierówność \(2x^2-7x+5 \ge 0\).

Wykaż, że liczba \(6^{100}-2 \cdot 6^{99}+10 \cdot 6^{98}\) jest podzielna przez \(17\).

Punkt \(S\) jest środkiem okręgu opisanego na trójkącie ostrokątnym \(ABC\). Kąt \(ACS\) jest trzy razy większy od kąta \(BAS\), a kąt \(CBS\) jest dwa razy większy od kąta \(BAS\). Oblicz kąty trójkąta \(ABC\).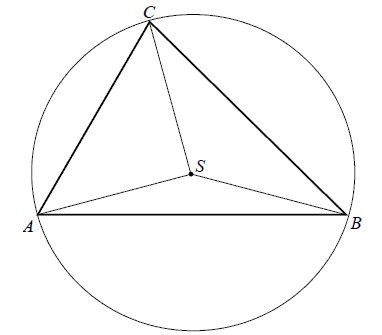

Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe \(100\) cm², a jego pole powierzchni bocznej jest równe \(260\) cm². Oblicz objętość tego ostrosłupa.

Dwa miasta łączy linia kolejowa o długości \(336\) kilometrów. Pierwszy pociąg przebył tę trasę w czasie o \(40\) minut krótszym niż drugi pociąg. Średnia prędkość pierwszego pociągu na tej trasie była o \(9\) km/h większa od średniej prędkości drugiego pociągu. Oblicz średnią prędkość każdego z tych pociągów na tej trasie.