Matura 2012 maj
Cenę nart obniżono o \(20\%\), a po miesiącu nową cenę obniżono o dalsze \(30\%\). W wyniku obu obniżek cena nart zmniejszyła się o
A.\(44\% \)
B.\(50\% \)
C.\(56\% \)
D.\(60\% \)
Liczba \(\sqrt[3]{{(-8)}^{-1}}\cdot {16}^{\frac{3}{4}}\) jest równa
A.\( -8 \)
B.\( -4 \)
C.\( 2 \)
D.\( 4 \)
Liczba \( {(3-\sqrt{2})}^{2}+4(2-\sqrt{2}) \) jest równa
A.\(19-10\sqrt{2} \)
B.\(17-4\sqrt{2} \)
C.\(15+14\sqrt{2} \)
D.\(19+6\sqrt{2} \)
Iloczyn \( 2\cdot \log_{\frac{1}{3}}9 \) jest równy
A.\(-6 \)
B.\(-4 \)
C.\(-1 \)
D.\(1 \)
Wskaż liczbę, która spełnia równanie \( |3x+1|=4x \).
A.\(x=-1 \)
B.\(x=1 \)
C.\(x=2 \)
D.\(x=-2 \)
Liczby \( {x}_{1}, {x}_{2} \) są różnymi rozwiązaniami równania \( 2x^2+3x-7=0 \). Suma \( {x}_{1}+{x}_{2} \) jest równa
A.\(-\frac{7}{2} \)
B.\(-\frac{7}{4} \)
C.\(-\frac{3}{2} \)
D.\(-\frac{3}{4} \)
Miejscami zerowymi funkcji kwadratowej \( y = -3(x-7)(x+2) \) są
A.\(x=7, x=-2 \)
B.\(x=-7, x=-2 \)
C.\(x=7, x=2 \)
D.\(x=-7, x=2 \)
Funkcja liniowa \( f \) jest określona wzorem \( f(x)=ax+6 \), gdzie \( a>0 \). Wówczas spełniony jest warunek
A.\(f(1)>1 \)
B.\(f(2)=2 \)
C.\(f(3)\lt 3 \)
D.\(f(4)=4 \)
Wskaż wykres funkcji, która w przedziale \( \langle -4, 4 \rangle \) ma dokładnie jedno miejsce zerowe. 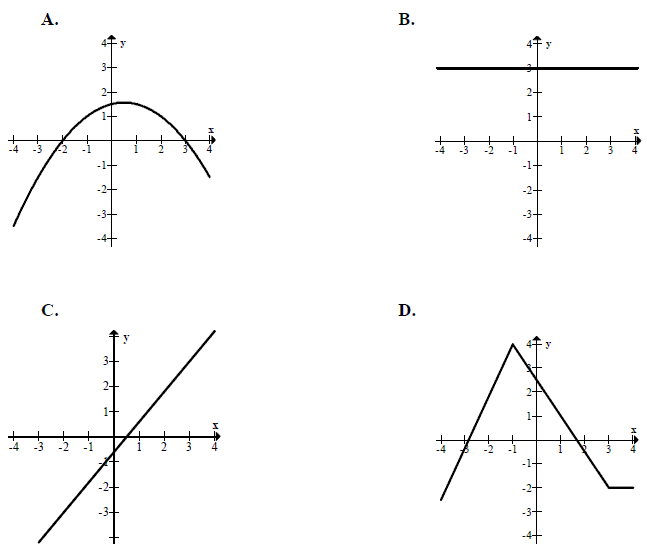

Liczba \( \operatorname{tg} 30^\circ -\sin 30^\circ \) jest równa
A.\(\sqrt{3}-1 \)
B.\(-\frac{\sqrt{3}}{6} \)
C.\(\frac{\sqrt{3}-1}{6} \)
D.\(\frac{2\sqrt{3}-3}{6} \)
W trójkącie prostokątnym \( ABC \) odcinek \( AB \) jest przeciwprostokątną i \( |AB|=13 \) oraz \( |BC|=12 \) . Wówczas sinus kąta \( ABC \) jest równy.
A.\(\frac{12}{13} \)
B.\(\frac{5}{13} \)
C.\(\frac{5}{12} \)
D.\(\frac{13}{12} \)
W trójkącie równoramiennym \( ABC \) dane są \( |AC|=|BC|=5 \) oraz wysokość \( |CD|=2 \). Podstawa \( AB \) tego trójkąta ma długość
A.\(6 \)
B.\(2\sqrt{21} \)
C.\(2\sqrt{29} \)
D.\(14 \)
W trójkącie prostokątnym dwa dłuższe boki mają długości \(5\) i \(7\). Obwód tego trójkąta jest równy
A.\(16\sqrt{6} \)
B.\(14\sqrt{6} \)
C.\(12+4\sqrt{6} \)
D.\(12+2\sqrt{6} \)
Odcinki \(AB\) i \(CD\) są równoległe i \( |AB|=5, |AC|=2, |CD|=7 \) (zobacz rysunek). Długość odcinka \( AE \) jest równa 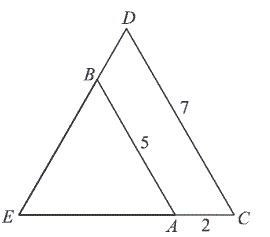

A.\(\frac{10}{7} \)
B.\(\frac{14}{5} \)
C.\(3 \)
D.\(5 \)
Pole kwadratu wpisanego w okrąg o promieniu \( 5 \) jest równe
A.\(25 \)
B.\(50 \)
C.\(75 \)
D.\(100 \)
Punkty \(A, B, C, D\) dzielą okrąg na \(4\) równe łuki. Miara zaznaczonego na rysunku kąta wpisanego \(ACD\) jest równa 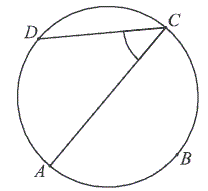

A.\( 90^\circ \)
B.\( 60^\circ \)
C.\( 45^\circ \)
D.\( 30^\circ \)
Miary kątów czworokąta tworzą ciąg arytmetyczny o różnicy \( 20^\circ \) . Najmniejszy kąt tego czworokąta ma miarę
A.\(40^\circ \)
B.\(50^\circ \)
C.\(60^\circ \)
D.\(70^\circ \)
Dany jest ciąg \( (a_n) \) określony wzorem \( a_n=(-1)^n\cdot \frac{2-n}{n^2} \) dla \( n\ge 1 \). Wówczas wyraz \( a_5 \) tego ciągu jest równy
A.\(-\frac{3}{25} \)
B.\(\frac{3}{25} \)
C.\(-\frac{7}{25} \)
D.\(\frac{7}{25} \)
Pole powierzchni jednej ściany sześcianu jest równe \( 4 \). Objętość tego sześcianu jest równa
A.\(6 \)
B.\(8 \)
C.\(24 \)
D.\(64 \)
Tworząca stożka ma długość \( 4 \) i jest nachylona do płaszczyzny podstawy pod kątem \( 45^\circ \). Wysokość tego stożka jest równa
A.\(2\sqrt{2} \)
B.\(16\pi \)
C.\(4\sqrt{2} \)
D.\(8\pi \)
Wskaż równanie prostej równoległej do prostej o równaniu \( 3x-6y+7=0 \)
A.\(y=\frac{1}{2}x \)
B.\(y=-\frac{1}{2}x \)
C.\(y=2x \)
D.\(y=-2x \)
Punkt \( A \) ma współrzędne \( (5, 2012) \). Punkt \( B \) jest symetryczny do punktu \( A \) względem osi \( Ox \), a punkt \( C \) jest symetryczny do punktu \( B \) względem osi \( Oy \) . Punkt \( C \) ma współrzędne
A.\((-5;-2012) \)
B.\((-2012;-5) \)
C.\((-5;2012) \)
D.\((-2012;5) \)
Na okręgu o równaniu \( (x-2)^2+(y+7)^2=4 \) leży punkt
A.\(A=(-2,5) \)
B.\(B=(2,-5) \)
C.\(C=(2,-7) \)
D.\(D=(7,-2) \)
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w \( 10 \) kolorach, jest równa 

A.\(100 \)
B.\(99 \)
C.\(90 \)
D.\(19 \)
Średnia arytmetyczna cen sześciu akcji na giełdzie jest równa \( 500 \) zł. Za pięć z tych akcji zapłacono \( 2300 \) zł. Cena szóstej akcji jest równa
A.\(400 \) zł
B.\(500 \) zł
C.\(600 \) zł
D.\(700 \) zł
Rozwiąż nierówność \(x^2 + 8x + 15 > 0\).
Uzasadnij, że jeśli liczby rzeczywiste \( a, b, c \) spełniają nierówności \( 0 \lt a \lt b \lt c \), to \( \frac{a+b+c}{3}>\frac{a+b}{2} \).
Liczby \(x_1 = -4\) i \(x_2 = 3\) są pierwiastkami wielomianu \(W(x) = x^3 + 4x^2 - 9x - 36\). Oblicz trzeci pierwiastek tego wielomianu.
Wyznacz równanie symetralnej odcinka o końcach \(A = (-2,2)\) i \(B = (2,10)\).
W trójkącie \(ABC\) poprowadzono dwusieczne kątów \(A\) i \(B\). Dwusieczne te przecinają się w punkcie \(P\). Uzasadnij, że kąt \(APB\) jest rozwarty.
Ze zbioru liczb \(\{1, 2, 3, 4, 5, 6, 7\}\) losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia \(A\), polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez \(6\).
Ciąg \((9, x, 19)\) jest arytmetyczny, a ciąg \((x, 42, y, z)\) jest geometryczny. Oblicz \(x\), \(y\) oraz \(z\).
W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60^\circ\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku. 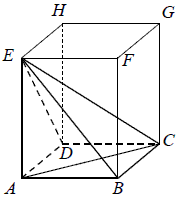

Miasto \(A\) i miasto \(B\) łączy linia kolejowa długości \(210\) km. Średnia prędkość pociągu pospiesznego na tej trasie jest o \(24\) km/h większa od średniej prędkości pociągu osobowego. Pociąg pospieszny pokonuje tę trasę o \(1\) godzinę krócej niż pociąg osobowy. Oblicz czas pokonania tej drogi przez pociąg pospieszny.