Matura 2011 listopad

Największa liczba naturalna \(n\) spełniająca nierówność \(n\lt 2\pi -1\) to:

Liczba \(\frac{\sqrt[4]{16}+\sqrt[3]{3\frac{3}{8}}}{\left (\frac{2}{7} \right)^{-1}}\) jest równa

Liczba \(\log 6\) jest równa

\(20\%\) pewnej liczby jest o \(16\) mniejsze od tej liczby. Tą liczbą jest

Rozwiązaniem równania \(-2=\frac{x-1}{x+2}\) jest liczba

Większa z liczb spełniających równanie \(x^2 + 6x + 8 = 0\) to

Przedział zaznaczony na osi liczbowej jest zbiorem rozwiązań nierówności

Dziedziną funkcji \(f(x)=\begin{cases} -2x+1,\quad \text{gdy } x\lt 1\\ -x,\quad \text{gdy } 1\le x\le 4 \end{cases} \) jest zbiór

Funkcja liniowa \(f(x)=(m+2)x+2m\) jest rosnąca, gdy

Rysunek przedstawia wykres funkcji \(y=f(x)\). 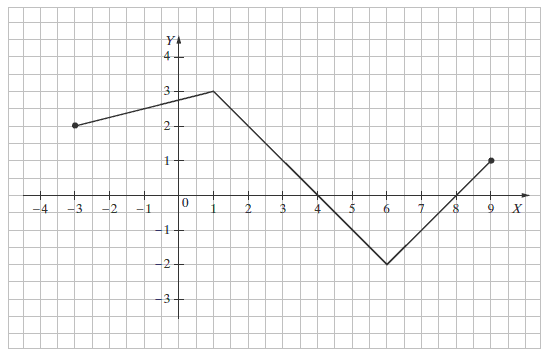Funkcja jest malejąca w przedziale

Punkt \(P=(a+1,2)\) należy do wykresu funkcji \(f(x)=\frac{4}{x}\). Liczba \(a\) jest równa

Do zbioru rozwiązań nierówności \(9\le x^2\) należy liczba

Wybierz i zaznacz równanie opisujące prostą prostopadłą do prostej o równaniu \(y=\frac{1}{2}x+1\).

Liczby \(x, 4, x+2\) są w podanej kolejności drugim, trzecim i czwartym wyrazem ciągu arytmetycznego. Wówczas liczba \(x\) jest równa

W ciągu geometrycznym \((a_n)\) są dane: \(a_2=-1, q=-2\). Suma czterech kolejnych początkowych wyrazów tego ciągu jest równa

Kąt \(\alpha \) jest ostry oraz \(\sin \alpha =\frac{2}{5}\). Wówczas

Dane są wielomiany \(W(x)=x^4-1\) oraz \(V(x)=x^4+1\). Stopień wielomianu \(W(x)+V(x)\) jest równy

Mediana danych: \(-4, 2, 6, 0, 1\) jest równa

Liczba punktów wspólnych okręgu o równaniu \((x-1)^2+y^2=4\) z prostą \(y=-1\) jest równa

Punkty \(A=(-2,-1)\) i \(B=(2,2)\) są wierzchołkami trójkąta równobocznego \(ABC\). Wysokość tego trójkąta jest równa

Dany jest okrąg o środku w punkcie \(S\). 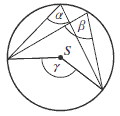Miara kąta \(\alpha \) jest równa \(70^\circ\). Oblicz sumę miar kątów \(\beta \) i \(\gamma \).

Trapez jest prostokątny. Trójkąty podobne \(ABD\) i \(CBD\) są równoramienne. 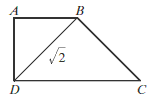Obwód trapezu jest równy

Graniastosłup ma \(2n+6\) wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa

Tworząca stożka jest o \(2\) dłuższa od promienia podstawy. Pole powierzchni bocznej tego stożka jest równe \(15\pi \). Tworząca stożka ma zatem długość

Cztery dziewczynki i sześciu chłopców siedzą na tym samym pniu zwalonego dębu. Dziewczynki siedzą obok siebie i chłopcy również siedzą obok siebie. Wszystkich możliwych sposobów posadzenia dzieci w ten sposób jest

Napisz równanie prostej równoległej do prostej o równaniu \(-3x+y-4=0\) i przechodzącej przez punkt \(P=(-1,-4)\).

W trójkącie prostokątnym jedna z przyprostokątnych ma długość \(a\). Kąt ostry przy tym boku ma miarę \(\alpha \). Wykaż, że \(\sin \alpha +\cos \alpha >1\).

Wykaż, że przekątna prostopadłościanu o krawędziach długości \(a, b, c\) ma długość \(\sqrt{a^2+b^2+c^2}\).

Rozwiąż nierówność \(x^2 + 5x \le 6\).

Wiadomo, że \(A\) i \(B\) są takimi zdarzeniami losowymi zawartymi w \(\Omega \), że \(P(A) = 0{,}7\), \(P(B)=0{,}6\) i \(P(A\cup B)=0{,}8\). Oblicz \(P(A \cap B)\).

Przekątna równoległoboku ma długość \(10\) cm i tworzy z krótszym bokiem kąt prosty, a z dłuższym bokiem kąt \(30^\circ\). Oblicz długość krótszego boku tego równoległoboku.

Okrąg wpisany w trójkąt prostokątny \(ABC\) jest styczny do przeciwprostokątnej \(AB\) w punkcie \(K\). Wiadomo, że \(|AK| = 4\) i \(|KB| = 6\). Oblicz promień tego okręgu.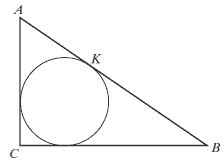

Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo tego, że liczba oczek otrzymana w pierwszym rzucie jest większa od liczby oczek otrzymanej w drugim rzucie?

Piramida ma kształt ostrosłupa prawidłowego czworokątnego, którego wysokość jest równa \(6\), a długość krawędzi bocznej jest równa \(2\sqrt{15}\). Oblicz miarę kąta nachylenia ściany bocznej piramidy do podstawy.