Logarytmy

Wprowadzenie do logarytmów

Drukuj

Poziom podstawowy

Logarytm wygląda następująco: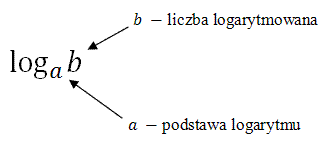

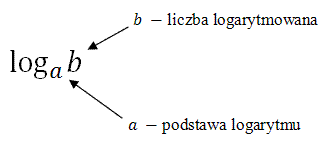Powyżej zapisany logarytm przeczytamy: "logarytm liczby \(b\) przy podstawie \(a\)" lub "logarytm przy podstawie \(a\) z liczby \(b\)".

W tym nagraniu wideo omawiam najważniejsze wiadomości dotyczące logarytmów.
Pokazuję najprostszą metodę obliczania logarytmów, omawiam wszystkie najważniejsze wzory związane z logarytmami, dziedzinę logarytmu oraz równania i nierówności logarytmiczne.

Czas nagrania: 67 min.

Poziom podstawowy

Definicja

Logarytmem liczby \(b\) przy podstawie \(a\) nazywamy taką liczbę \(x\), że \(a\) podniesione do potęgi \(x\) daje liczbę \(b\): \[\log_a b = x\quad \Leftrightarrow \quad a^x=b\]

Zatem żeby obliczyć \(\log_a b \), wystarczy odpowiedzieć na pytanie:

Do jakiej potęgi podnieść liczbę \(a\), żeby otrzymać liczbę \(b\)?

W poniższej tabelce podamy jeszcze raz definicję logarytmu oraz jego interpretację.

Jak zapisujemy	Jak czytamy	Jak rozumiemy
\[\log_a b \]	logarytm liczby b przy podstawie a	Do jakiej potęgi podnieść liczbę a, żeby otrzymać liczbę b

Logarytm istnieje tylko wówczas, gdy spełnione są trzy warunki, które często nazywamy założeniami lub dziedziną logarytmu:

podstawa logarytmu musi być zawsze liczbą dodatnią, czyli: \(a>0\),
podstawa jest różna od \(1\), zatem: \(a\ne 1\),
liczba logarytmowana musi być dodatnia, czyli: \(b>0\).

Sposoby liczenia logarytmów zostały również omówione w dziale Obliczanie logarytmów.