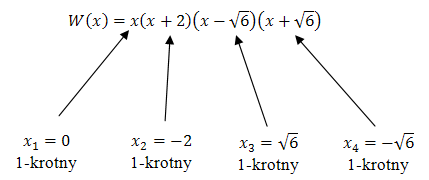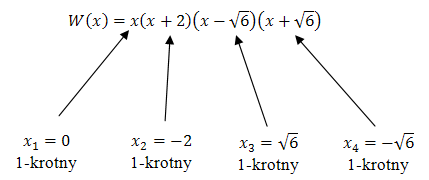Krotność pierwiastka wielomianu

Poziom rozszerzony

Do wyznaczenia pierwiastków wielomianu oraz ich krotności, należy rozłożyć wielomian na iloczyn czynników.
Wówczas krotność pierwiastka wielomianu, to najwyższa potęga nawiasu, który zeruje dany pierwiastek.

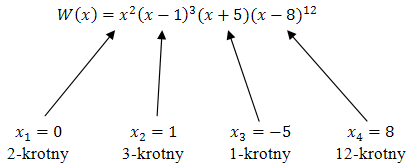
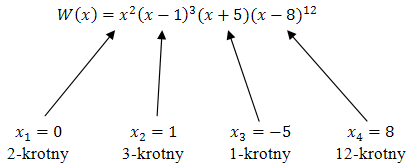
Dla wielomianu zapisanego w postaci iloczynowej łatwo jest odczytać pierwiastki i ich krotności. Na przykład:

Dla wielomianu \(w(x) = (x + 2)^7(x + 11)^3(x - 5)^2\) wyznacz pierwiastki oraz ich krotności.

Pierwiastki wielomianu wyznaczamy rozwiązując równanie wielomianowe: \[ (x + 2)^7(x + 11)^3(x - 5)^2 = 0\\[6pt] x + 2 = 0 \quad \lor \quad x + 11 = 0 \quad \lor \quad x - 5 = 0\\[6pt] x = -2 \quad \lor \quad x = -11 \quad \lor \quad x = 5 \] Teraz określamy krotności tych pierwiastków: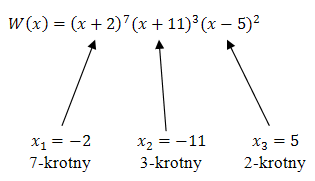

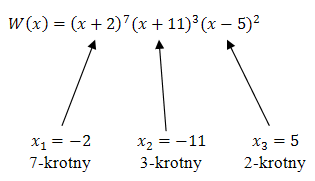
Dla wielomianu \(w(x) = x^3(x - 1)^{10}(x + 2)^9(x + 1)^8\) wyznacz pierwiastki i określ ich krotności.

Pierwiastki wielomianu wyznaczamy rozwiązując równanie wielomianowe:

\[ x^3(x - 1)^{10}(x + 2)^9(x + 1)^8 = 0\\[6pt] x = 0 \ \lor \ x - 1 = 0 \ \lor \ x + 2 = 0\ \lor \ x + 1 = 0\\[6pt] x = 0 \ \lor \ x = 1 \ \lor \ x = -2\ \lor \ x = -1 \]

Teraz określamy krotności tych pierwiastków: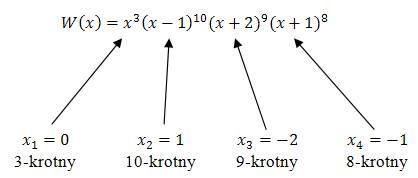

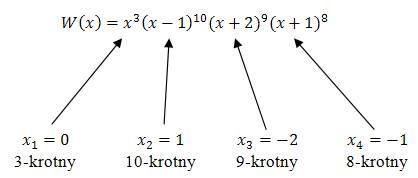
Wyznacz pierwiastki wielomianu \(w(x) = x^2(x - 1)(x + 1)\) i określ ich krotności.

Pierwiastki wielomianu wyznaczamy rozwiązując równanie wielomianowe: \[ x^2(x - 1)(x + 1) = 0\\[6pt] x = 0 \quad \lor \quad x - 1 = 0 \quad \lor \quad x + 1 = 0\\[6pt] x = 0 \quad \lor \quad x = 1 \quad \lor \quad x = -1 \] Teraz określamy krotności tych pierwiastków: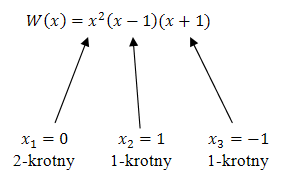

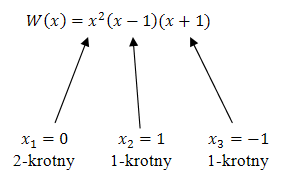
Wyznacz pierwiastki wielomianu \(w(x) = x^4 + 2x^3 - 6x^2 - 12x\) i określ ich krotności.

Pierwiastki wielomianu wyznaczamy rozwiązując równanie wielomianowe:

\[ x^4 + 2x^3 - 6x^2 - 12x = 0\\[6pt] x(x^3 + 2x^2 - 6x - 12) = 0\\[6pt] x(x^2(x + 2) - 6(x + 2)) = 0\\[6pt] x(x + 2)(x^2 - 6) = 0\\[6pt] x(x + 2)(x - \sqrt{6})(x + \sqrt{6}) = 0\\[6pt] x = 0 \ \lor \ x +2 = 0 \ \lor \ x -\sqrt{6} = 0\ \lor \ x +\sqrt{6} = 0\\[6pt] x = 0 \ \lor \ x = -2 \ \lor \ x = \sqrt{6}\ \lor \ x = -\sqrt{6} \]

Teraz zapisujemy wielomian w postaci iloczynowej i określamy krotności pierwiastków: