Jesteś tutaj: Szkoła → Funkcja logarytmiczna
Funkcja logarytmiczna
1.
Wprowadzenie do funkcji logarytmicznejWprowadzenie do funkcji logarytmicznej
Funkcja logarytmiczna ma wzór: \[f(x)=\log_ax\] Zakładamy przy tym, że \(a \gt 0\), \(a\ne 1\), \(x\gt 0\).
Wykresem tej funkcji jest krzywa która zawsze przecina oś \(Ox\) dla argumentu \(x = 1\).Zasadniczy kształt wykresu zależy do tego czy \(a \gt 1\) czy \(a \lt 1\). Pokażemy oddzielnie te dwa przypadki.
Narysujemy wykres funkcji \(f(x) = \log_2x\).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
Zatem wykres tej funkcji będzie wyglądał następująco: 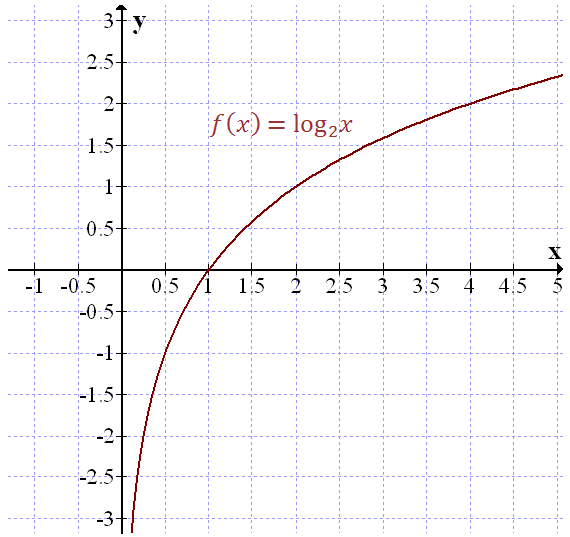
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
| \(x\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(4\) |
| \(y=\log_2x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |

Bardzo podobnie wyglądają wykresy innych funkcji logarytmicznych o podstawie \(a \gt 1\). Przykładowo: 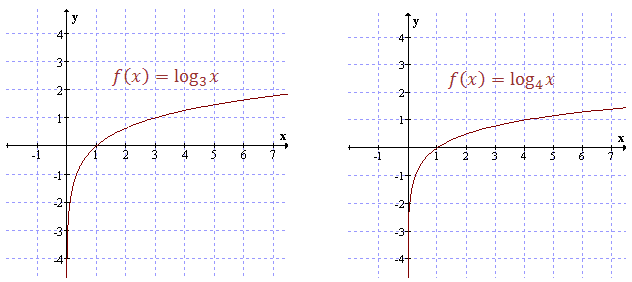 Własności funkcji logarytmicznej o podstawie \(a \gt 1\):
Własności funkcji logarytmicznej o podstawie \(a \gt 1\):
Teraz zobaczymy jak wyglądają funkcje logarytmiczne o podstawie \(a \lt 1\).  Własności funkcji logarytmicznej o podstawie \(a \gt 1\):
Własności funkcji logarytmicznej o podstawie \(a \gt 1\): - Dziedzina: \(\mathbb{R}^+ \).
- Zbiór wartości: \(\mathbb{R} \).
- Monotoniczność: funkcja jest rosnąca.
- Różnowartościowość: funkcja jest różnowartościowa.
- Miejsca zerowe: \(x = 1\).
- Parzystość: nie jest.
- Nieparzystość: nie jest.
Narysujemy wykres funkcji \(f(x) = \log_{\frac{1}{2}}x\).
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
Zatem wykres tej funkcji będzie wyglądał następująco: 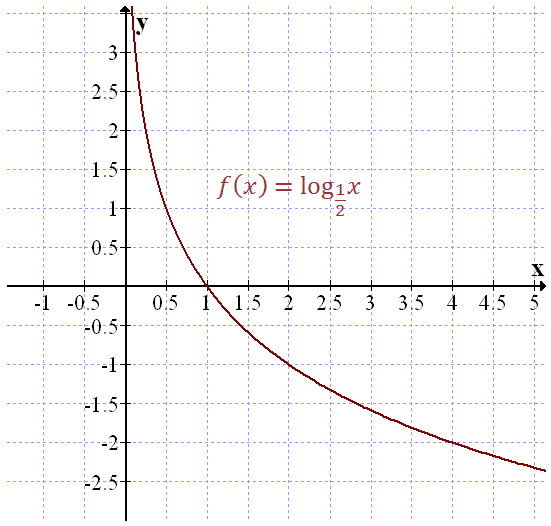
Na początek obliczmy wartości tej funkcji dla kilku przykładowych argumentów \(x\). Sporządźmy zatem odpowiednią tabelkę:
| \(x\) | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(1\) | \(2\) | \(4\) |
| \(y=\log_{\frac{1}{2}}x\) | \(2\) | \(1\) | \(0\) | \(-1\) | \(-2\) |

Bardzo podobnie wyglądają wykresy innych funkcji logarytmicznych o podstawie \(a \lt 1\). Przykładowo: 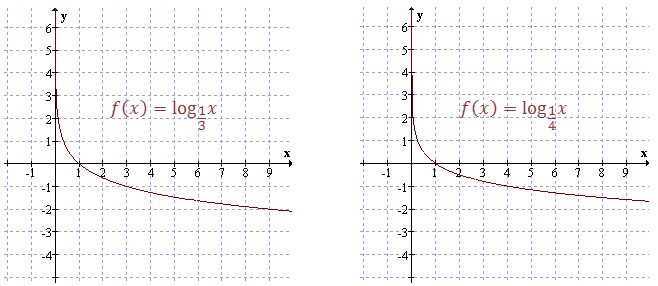 Własności funkcji logarytmicznej o podstawie \(a \lt 1\):
Własności funkcji logarytmicznej o podstawie \(a \lt 1\):
 Własności funkcji logarytmicznej o podstawie \(a \lt 1\):
Własności funkcji logarytmicznej o podstawie \(a \lt 1\): - Dziedzina: \(\mathbb{R}^+ \).
- Zbiór wartości: \(\mathbb{R}\).
- Monotoniczność: funkcja jest malejąca.
- Różnowartościowość: funkcja jest różnowartościowa.
- Miejsca zerowe: \(x = 1\).
- Parzystość: nie jest.
- Nieparzystość: nie jest.