Funkcja liniowa - zadania z parametrem
Poziom podstawowy
Punkt \(A=(0, 1)\) leży na wykresie funkcji liniowej \(f(x)=(m-2)x+m-3\). Stąd wynika, że
A.\( m=1 \)
B.\( m=2 \)
C.\( m=3 \)
D.\( m=4 \)
Wskaż \(m\), dla którego funkcja liniowa \(\ f(x)=(m−1)x+6\ \) jest rosnąca
A.\( m=-1 \)
B.\( m=0 \)
C.\( m=1 \)
D.\( m=2 \)
Wskaż \(m\), dla którego funkcja liniowa określona wzorem \(\ f(x)=(m - 1)x+3\ \) jest stała.
A.\( m=1 \)
B.\( m=2 \)
C.\( m=3 \)
D.\( m=-1 \)
Funkcja liniowa \(f(x)=(m^2-1)x-7\) jest malejąca, jeśli:
A.\( m\in \mathbb{R} \)
B.\( m\in (-\infty , -1) \)
C.\( m\in (-1, 1) \)
D.\( m\in (-\infty , 0) \)
Funkcja \(f\) jest określona wzorem \(f(x)=5x-m\), gdzie \(m\lt 0\). Wówczas spełniony jest warunek
A.\( f(1)\lt 0 \)
B.\( f(2)>10 \)
C.\( f(3)<-3 \)
D.\( f(4)=20 \)
Prosta o równaniu \(y=-2x+(3m+3)\) przecina w układzie współrzędnych oś \(Oy\) w punkcie \((0,2)\). Wtedy
A.\( m=-\frac{2}{3} \)
B.\( m=-\frac{1}{3} \)
C.\( m=\frac{1}{3} \)
D.\( m=\frac{5}{3} \)
Funkcja liniowa \( f \) jest określona wzorem \( f(x)=ax+6 \), gdzie \( a>0 \). Wówczas spełniony jest warunek
A.\(f(1)>1 \)
B.\(f(2)=2 \)
C.\(f(3)\lt 3 \)
D.\(f(4)=4 \)
Dana jest funkcja \(f(x) = (1 + m^2)x - 5\). Oblicz współczynnik \(m\) jeżeli wiadomo, że \(x = 1\) jest miejscem zerowym funkcji \(f(x)\).
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (m - 1)x + 5\) jest
- rosnąca
- równoległa do prostej \(y = -6x + 3\)
Wyznacz wszystkie parametry \(m\) dla których prosta o równaniu \(y = (3 - 2m)x + 5\) jest
- malejąca
- prostopadła do prostej \(y = 2x-3\)
Miejscem zerowym funkcji liniowej \(f(x)=-2x+m+7\) jest liczba \(3\). Wynika stąd, że
A.\( m=7 \)
B.\( m=1 \)
C.\( m=-1 \)
D.\( m=-7 \)
Proste o równaniach \(y=2x-5\) i \(y=(3-m)x+4\) są równoległe. Wynika stąd, że
A.\( m=1 \)
B.\( m=\frac{5}{2} \)
C.\( m=\frac{7}{2} \)
D.\( m=5 \)
Funkcja liniowa \(f(x)=(m-2)x-11\) jest rosnąca dla
A.\( m>2 \)
B.\( m>0 \)
C.\( m\lt 13 \)
D.\( m\lt 11 \)
Liczba \( 1 \) jest miejscem zerowym funkcji liniowej \( f(x)=(2-m)x+1 \). Wynika stąd, że
A.\(m=0 \)
B.\(m=1 \)
C.\(m=2 \)
D.\(m=3 \)
Rysunek przedstawia wykres funkcji \(y=f(x)\).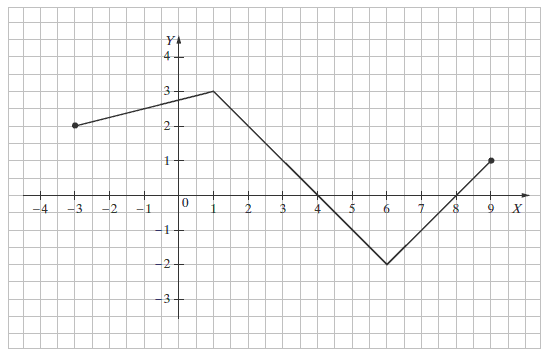 
Funkcja jest malejąca w przedziale
Funkcja jest malejąca w przedziale A.\( \langle 0,4 \rangle \)
B.\( \langle 1,6 \rangle \)
C.\( \langle 0,6 \rangle \)
D.\( \langle -2,4 \rangle \)
Na wykresie funkcji liniowej określonej wzorem \(f(x)=(m-1)x+3\) leży punkt \(S=(5,-2)\). Zatem
A.\( m=1 \)
B.\( m=2 \)
C.\( m=-1 \)
D.\( m=0 \)
Punkt \(M=\left ( \frac{1}{2},3 \right )\) należy do wykresu funkcji liniowej określonej wzorem \(f(x)=(3-2a)x+2\). Wtedy
A.\( a=-\frac{1}{2} \)
B.\( a=2 \)
C.\( a=\frac{1}{2} \)
D.\( a=-2 \)
Punkt \(A=\left(\frac{1}{3},-1\right)\) należy do wykresu funkcji liniowej \(f\) określonej wzorem \(f(x)=3x+b\). Wynika stąd, że
A.\( b=2 \)
B.\( b=1 \)
C.\( b=-1 \)
D.\( b=-2 \)
Funkcja liniowa \(f(x)=(m+2)x+2m\) jest rosnąca, gdy
A.\( m<-2 \)
B.\( m\lt 2 \)
C.\( m>-2 \)
D.\( m>-4 \)
Dana jest funkcja \(h(x)=\left ( -\frac{1}{3}m+2 \right)x+\frac{3}{2}m-1\). Funkcja ta dla argumentu \(0\) przyjmuje wartość \(5\). Wówczas:
A.\( m=9 \)
B.\( m=6 \)
C.\( m=4 \)
D.\( m=2 \)
Do wykresu funkcji \(f(x)=(m-1)x+m^2+1\) należy punkt \(P=(0,5)\). Parametr \(m\) może być równy
A.\( 0 \)
B.\( 1 \)
C.\( 2 \)
D.\( \sqrt{6} \)
Funkcje liniowe \(f\) i \(g\) określone wzorami \(f(x) =-4x + 12\) i \(g(x) =-2x + k + 3\) mają wspólne miejsce zerowe. Stąd wynika, że
A.\( k=-6 \)
B.\( k=-3 \)
C.\( k=3 \)
D.\( k=6 \)
Funkcja liniowa \(f(x)=(a-1)x+3\) osiąga wartość najmniejszą równą \(3\). Wtedy
A.\( a=-1 \)
B.\( a=0 \)
C.\( a=1 \)
D.\( a=3 \)
Tematy nadrzędne i sąsiednie