Długość odcinka w układzie współrzędnych
Wzór
Długość odcinka o końcach w punktach \(A=(x_1,y_1)\) oraz \(B=(x_2,y_2)\) obliczamy ze wzoru: \[|AB|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\]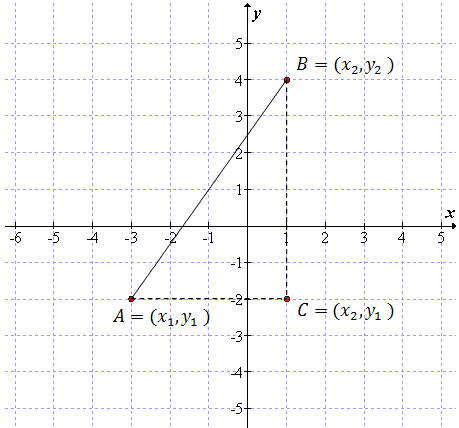
Wzór na długość odcinka można wyprowadzić z twierdzenia Pitagorasa dla trójkąta prostokątnego \(ABC\):
\[\begin{split} |AB|^2&=|AC|^2+|BC|^2\\[6pt] |AB|&=\sqrt{|AC|^2+|BC|^2}\\[6pt] |AB|&=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} \end{split}\] Dane są punkty \(P=(-2,-2)\), \(Q=(3,3)\). Odległość punktu \(P\) od punktu \(Q\) jest równa
A.\( 1 \)
B.\( 5 \)
C.\( 5\sqrt{2} \)
D.\( 2\sqrt{5} \)
Długość odcinka \( AB \), którego wierzchołki mają współrzędne \( A=(-3,-2) \) i \( B=(-1,4) \), jest równa
A.\(2\sqrt{5} \)
B.\(2\sqrt{10} \)
C.\(4\sqrt{2} \)
D.\(\sqrt{41} \)
Dane są punkty \(A=(1,-4)\) i \(B=(2,3)\). Odcinek \(AB\) ma długość
A.\( 1 \)
B.\( 4\sqrt{3} \)
C.\( 5\sqrt{2} \)
D.\( 7 \)
Na okręgu o środku \(S=(-6,1)\) leży punkt \(A=(-2,4)\). Promień tego okręgu jest równy
A.\(5\)
B.\(7\)
C.\(\sqrt{73}\)
D.\(\sqrt{7}\)
Punkty \(B = (−2, 4)\) i \(C = (5, 1)\) są dwoma sąsiednimi wierzchołkami kwadratu \(ABCD\). Pole tego kwadratu jest równe
A.\( 74 \)
B.\( 58 \)
C.\( 40 \)
D.\( 29 \)
Punkty \( A=(-1,3)\) i \(C=(7,9) \) są przeciwległymi wierzchołkami prostokąta \( ABCD \). Promień okręgu opisanego na tym prostokącie jest równy
A.\(10 \)
B.\(6\sqrt{2} \)
C.\(5 \)
D.\(3\sqrt{2} \)
Punkty \(A=(1,-2)\), \(C=(4,2)\) są dwoma wierzchołkami trójkąta równobocznego \(ABC\). Wysokość tego trójkąta jest równa
A.\( \frac{5\sqrt{3}}{2} \)
B.\( \frac{5\sqrt{3}}{3} \)
C.\( \frac{5\sqrt{3}}{6} \)
D.\( \frac{5\sqrt{3}}{9} \)
Punkty \(A=(-3,-1)\), \(B=(2,5)\) są dwoma wierzchołkami trójkąta równobocznego \(ABC\). Pole tego trójkąta jest równe
A.\( \frac{\sqrt{183}}{2} \)
B.\( \frac{61\sqrt{3}}{2} \)
C.\( \frac{61\sqrt{3}}{4} \)
D.\( \frac{11\sqrt{3}}{4} \)
Punkty \(B=(0,0)\), \(C=(3,0)\) są dwoma wierzchołkami trójkąta równobocznego \(ABC\). Obwód tego trójkąta jest równy
A.\( 3 \)
B.\( 9 \)
C.\( \frac{3\sqrt{3}}{2} \)
D.\( \frac{9\sqrt{3}}{4} \)
Punkty \( A=(-1,2) \) i \( B=(2,6) \) są wierzchołkami kwadratu \( ABCD \). Pole tego kwadratu jest równe:
A.\(17 \)
B.\(65 \)
C.\(25 \)
D.\(7 \)
Dany jest okrąg o środku \(S=(−6,−8)\) i promieniu \(2014\). Obrazem tego okręgu w symetrii osiowej względem osi \(Oy\) jest okrąg o środku w punkcie \(S_1\). Odległość między punktami \(S\) i \(S_1\) jest równa
A.\( 12 \)
B.\( 16 \)
C.\( 2014 \)
D.\( 4028 \)
Punkty \(E = (7,1)\) i \(F = (9,7)\) to środki boków, odpowiednio \(AB\) i \(BC\) kwadratu \(ABCD\). Przekątna tego kwadratu ma długość
A.\( 4\sqrt{5} \)
B.\( 10 \)
C.\( 4\sqrt{10} \)
D.\( 20 \)